一维弹性碰撞的基本结论以及柯尼希定理的应用
碰撞是生活中很常见的运动现象，物体的碰撞一般只涉及两个物体，根据两物体的碰撞情况，可以分为一维碰撞和二维碰撞，在高中阶段，只研究一维碰撞，我们将两物体碰撞前后速度在一条直线上的碰撞称为一维碰撞，根据碰撞前后两物体组成的系统能量损失不同，分为弹性碰撞、非弹性碰撞、完全非弹性碰撞三类。
弹性碰撞：碰撞前后无机械能损失的碰撞。（动量守恒，机械能守恒）
非弹性碰撞：碰撞前后有机械能损失的碰撞。（动量守恒，机械能不守恒）
完全非弹性碰撞：碰撞前后有机械能损失，并且机械能损失最大。（动量守恒，机械能损失最大）
一、两小球一维弹性碰撞中的一般性规律
如下图，质量分别为 $m_1$ 和 $m_2$ 小球在光滑的水平面上，分别以速度 $v_1$ 和 $v_2$ 发生弹性碰撞，设 $m_1$ 碰撞后的速度为 $v_1^{'}$ ，$m_2$ 碰撞后的速度为 $v_2^{'}$。
动量守恒：
$$ m_1 v_1 + m_2 v_2 = m_1 v_1^{'} + m_2 v_2^{'} \quad (1) $$机械能守恒：
$$ \frac{1}{2} m_1 v_1^2 + \frac{1}{2} m_2 v_2^2 = \frac{1}{2} m_1 {v_1^{'}}^2 + \frac{1}{2} m_2 {v_2^{'}}^2 \quad (2) $$由（1）式子可得：
$$ m_1(v_1 - v_1^{'}) = m_2(v_2^{'} - v_2) \quad (3) $$由（2）式子可得：
$$ m_1(v_1^2 - {v_1^{'}}^2) = m_2({v_2^{'}}^2 - v_2^2) $$化简可得：
$$ m_1(v_1 + v_1^{'})(v_1 - v_1^{'}) = m_2(v_2 + v_2^{'})(v_2^{'} - v_2) \quad (4) $$由 $\frac{(4)}{(3)}$ 可得：
$$ v_1 + v_1^{'} = v_2 + v_2^{'} $$移项可得：
$$ v_1 - v_2 = v_2^{'} - v_1^{'} \quad (5) $$从（5）式可知：两小球弹性碰撞前后的相对速度大小相等。
联立（1）和（5）可得：
$$ v_1^{'} = \frac{(m_1 - m_2)v_1 + 2m_2v_2}{m_1 + m_2} \quad (6) $$ $$ v_2^{'} = \frac{(m_2 - m_1)v_2 + 2m_1v_1}{m_1 + m_2} \quad (7) $$如果两小球是完全非弹性碰撞，碰撞后的共同速度 $v_{\text{共}} = \frac{m_1 v_1 + m_2 v_2}{m_1 + m_2} \quad (8)$
联立 (6)(7)(8) 三式可得：
$$ v_1^{'} = 2v_{\text{共}} - v_1 \quad v_2^{'} = 2v_{\text{共}} - v_2 $$可知：每个小球碰撞前后的速度关于共速的速度对称。
对下面碰撞后的速度分析：
$$ v_1^{'} = \frac{(m_1 - m_2)v_1 + 2m_2v_2}{m_1 + m_2} $$ $$ v_2^{'} = \frac{(m_2 - m_1)v_2 + 2m_1v_1}{m_1 + m_2} $$- 当 $v_2 = 0$，为高考中最常见的一动碰一静问题，
- 当 $m_1 = m_2$，
- 引入碰撞恢复系数 $e = \frac{v_2^{'} - v_1^{'}}{v_1 - v_2}$。当 $e = 1$ 时，碰撞为弹性碰撞；当 $e = 0$ 时，碰撞为完全非弹性碰撞；当 $e < 1$ 时，碰撞为非弹性碰撞。引入恢复系数可以得到碰撞过程中两小球损失的动能：
二、引入质心分析碰撞过程
对于 $m_1$、$m_2$ 物体组成的二体系统，质心位置
$$ r_c = \frac{m_1 r_1 + m_2 r_2}{m_1 + m_2} $$ 质心速度 $$ v_c = \frac{m_1 v_1 + m_2 v_2}{m_1 + m_2} $$ 质心加速度 $$ a_c = \frac{m_1 a_1 + m_2 a_2}{m_1 + m_2}. $$两小球碰撞的过程中，动量守恒，两小球系统外力为零，质心加速度为零，质心做匀速直线运动。当以质心为参考系时，两小球系统总动量为零，下面刘叔物理用柯尼希定理来分析碰撞过程。
根据柯尼希定理：两小球系统的动能等于质心的动能加上两小球相对质心的动能和。
$$ \frac{1}{2} m_1 v_1^2 + \frac{1}{2} m_2 v_2^2 = \frac{1}{2} (m_1 + m_2) v_c^2 + \frac{1}{2} m_1 (v_1 - v_c)^2 + \frac{1}{2} m_2 (v_2 - v_c)^2 $$其中
$$ \frac{1}{2} m_1 (v_1 - v_c)^2 + \frac{1}{2} m_2 (v_2 - v_c)^2 = \frac{1}{2} \frac{m_1 m_2}{m_1 + m_2}(v_1 - v_2)^2 $$柯尼希定理也可以写成
$$ \frac{1}{2} m_1 v_1^2 + \frac{1}{2} m_2 v_2^2 = \frac{1}{2} (m_1 + m_2) v_c^2 + \frac{1}{2} \frac{m_1 m_2}{m_1 + m_2} (v_1^{'} - v_2^{'})^2 $$其中 $E_{kc} = \frac{1}{2} (m_1 + m_2) v_c^2$ 称为质心动能；$E_{kr} = \frac{1}{2} \frac{m_1 m_2}{m_1 + m_2} (v_1^{'} - v_2^{'})^2$ 称为资用能。$\frac{m_1 m_2}{m_1 + m_2}$ 称为约化质量（或者叫折合质量）。
- 当发生弹性碰撞时，两球碰撞前后的相对速度大小不变，即
-
当发生完全非弹性碰撞时，$v_1^{'} = v_2^{'}$，$E_{kr} = 0$，资用能完全损失掉。
-
当发生非弹性碰撞时，$|v_1^{'} - v_2^{'}| < |v_2 - v_1|$，资用能部分损失。
可以看出，碰撞过程中，质心动能不会损失，损失的是资用能；利用这些结论，可以快速求解二体系统动量守恒很多问题，下面刘叔物理用几个例题来说明利用柯尼希定理解决相关问题的快捷性。
三、例题的运用
- 如图所示，质量 $m_1 = 3, \text{kg}$ 且足够长的小车静止在光滑的水平面上，现有质量 $m_2 = 2, \text{kg}$ 可视为质点的物块，以水平向右的速度 $v_0 = 2 , \text{m/s}$ 从左端滑上小车，物块与车上表面间的动摩擦因数 $\mu = 0.5$，最后恰好不掉下小车且与小车保持相对静止， $g$ 取 $10 , \text{m/s}^2$，求这一过程中系统损失的机械能。
根据柯尼希定理：
$$ \frac{1}{2} m_1 v_1^2 + \frac{1}{2} m_2 v_2^2 = \frac{1}{2} (m_1 + m_2) v_c^2 + \frac{1}{2} \frac{m_1 m_2}{m_1 + m_2} (v_1^{'} - v_2^{'})^2 $$对这小车和物块满足：
$$ \frac{1}{2} m_2 v_0^2 = \frac{1}{2} (m_1 + m_2) v_c^2 + \frac{1}{2} \frac{m_1 m_2}{m_1 + m_2} v_0^2 $$当两球相对速度为零时，损失的动能最大，资用能全部转化为热能，
$$ Q = \frac{1}{2} \frac{m_1 m_2}{m_1 + m_2} v_0^{2} = 2.4 \, J $$- 如图所示，在固定的光滑水平杆上，套有质量为 $m$ 的光滑圆环，轻绳一端拴在环上，另一端系着质量也为 $m$ 的木块，现有质量为 $m$ 的子弹以大小为 $v$ 的水平速度射入木块并立刻留在木块中，不计空气阻力，重力加速度为 $g$，求子弹射入木块后子弹和木块能上升的最大高度。
根据动量守恒，
$$ m_0 \cdot v = (m_0 + m) v \quad \Rightarrow \quad v = \frac{m_0 v}{m_0 + m} $$资用能则为
$$ Q = \frac{1}{2} \frac{m_0 m}{m_0 + m} v_0^{2} $$碰撞后对 $m_0$、木块 $m$、圆环 $m$ 分析，子弹和木块达到最高点的过程中，资用能全部转化为重力势能，即
$$ \frac{1}{2} \frac{(m_0 + m)m}{m_0 + 2m} v^{2} = (m_0 + m)gh $$解得
$$ h = \frac{m m_0^2 v_0^2}{2g(m_0 + m)^2(m_0 + 2m)} $$- 如图(a)，一质量为 $m$ 的物块A与轻质弹簧连接，静止在光滑水平面上，物块B向A 运动，$t=0$ 时与弹簧接触，到 $t=2t_0$ 时与弹簧分离，第一次碰撞结束，A、B 的 $v-t$ 图像 如图（b）所示。已知从 $t=0$ 到 $t=t_0$ 时间内，物块A运动的距离为 $0.36v_0t_0$。A、B 分离后，A滑上粗糙斜面，然后滑下，与一直在水平面上运动的B再次碰撞，之后 A 再次滑上斜面，达到的最高点与前一次相同。斜面倾角为 $\theta (\sin \theta = 0.6)$，与水平面光滑连接。
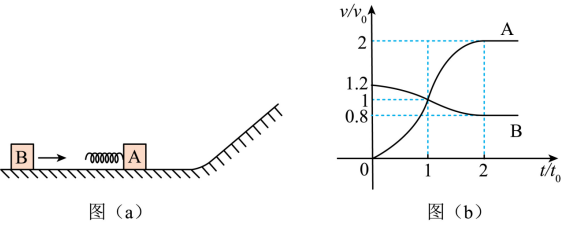
求 (1) 第一次碰撞过程中，弹簧弹性势能的最大值。
(2) 第一次碰撞过程中，弹簧压缩量的最大值。
解：(1) 首先，碰撞过程中根据动量守恒求出 B 的质量 $m_B$。
$$ m_B \cdot 1.2v_0 = (m_B + m)v_0 \quad \Rightarrow \quad m_B = 5m $$弹簧弹性势能的最大值时，资用能全部转化为弹性势能
$$ E_k = \frac{1}{2} \frac{m \cdot 5m}{(m + 5m)}(1.2v_0)^2 = 0.6 mv_0^2 $$(2) 对两物块组成的系统，质心位移满足：
$$ x_c = \frac{m_A x_A + m_B x_B}{m_A + m_B} $$质心速度满足：
$$ v_c = \frac{m_A v_A + m_B v_B}{m_A + m_B}, \quad x_c = v_c t $$代入相关数据可得弹簧压缩量的最大值：
$$ \Delta x = x_B - x_A = 0.768v_0 t_0 $$柯尼希定理和质心相关的知识，属于高考超纲内容，在计算题中是不能直接运用的，但我们可以按步骤写相关的公式，利用柯尼希定理和质心相关知识快速得出答案，将会很大程度提高解题速度。
高中物理知识点总结