本文针对知识保留水平为 95% 的配对联想学习，确定了一个计算重复间隔的通用公式。
据称，该公式可广泛应用于各种学科的学习实践中，且不受个体学习者能力的限制。

翻译对原文的表述做了一些改动

关于此文章

此文章所使用的论文的原标题是: Optimization of repetition spacing in the practice of learning
翻译对原文的表述做了一些改动
原始 PDF 文档在 此处 可以下载 (镜像)
论文原始作者是 Piotr A. Woiniak 和 Edward J. Gorzelanczyk (来自波兹南医学院组织胚胎学系)
这篇文章的相关原理将运用到辅助记忆软件中

摘要

本文针对知识保留水平为 95% 的配对联想学习，确定了一个计算重复间隔的通用公式。
据称，该公式可广泛应用于各种学科的学习实践中，且不受个体学习者能力的限制。

研究思路

许多出版物都广泛讨论了不同重复间隔对学习效果的影响。特别是，间隔效应被认为是一种普遍现象。间隔效应是指，如果重复的间隔是分散/稀疏的，而不是集中重复，那么学习任务的表现会更好。因此，有观点提出，学习中使用的最佳重复间隔是最长的、但不会导致遗忘的间隔。然而，遗忘具有随机性，因此无法预测它何时会在特定情况下发生。所以，尽管进行了多次尝试，但很少有研究提出可在学习实践中使用的重复间隔。

在本研究中，我们采用了一种随机方法。我们通过将最佳间隔定义为导致少量（预先确定）学习材料被遗忘的间隔来计算最佳重复间隔。我们使用了一个计算机程序来监控学习过程，确保在重复时只有 5% 的待记忆项目未被记住。该程序采用了一种优化算法，当遗忘项目的比例低于或高于所需 5% 的水平时，它会自动延长或缩短重复间隔。

此外，在学习过程中，待记忆项目根据受试者的表现自动分为不同的难度类别。对于每个难度类别，我们都应用了不同的重复间隔。

实验过程

参与实验的受试者是波兹南工业大学的 7 名计算机科学系本科生，他们是无偿志愿者。在 18 个月的时间里，他们总共记忆和重复了超过 35000 个他们选择的项目（这些项目是波兰语-英语单词对）。这些记忆的项目是受试者在实验前不认识的。受试者在 2 个月内使用下述算法分批掌握了所有材料，并在接下来的 16 个月内继续重复。

算法中的每次重复过程如下：

呈现问题

受试者尝试回答

将回答与正确答案进行比较

受试者进行 0-5 分的自我评估（0 分 - 非常差，5 分 - 非常好）

用于确定最佳重复间隔的函数（最佳间隔函数）以表格形式的最佳因子矩阵表示.

(1) 式:

$$ I(EF, 1) = OF(EF, 1) $$

(2) 式:

$$ I(EF, R) = I(EF, R - 1) * OF(EF, R) $$

公式中: $ EF $ - 简单度因子，用于反映该项目被记忆的难易程度 $ I(EF,R) $ - 间隔 (单位: 天)，对于简单度因子确定为 EF 的项目，在第 R 次重复之前的间隔 $ OF(EF, R) $ - 最优间隔函数 表一

为了更好地拟合最优间隔因子，我们使用了一种优化算法来修改矩阵 OF 的初始值，主要判据是稳定的知识保留率达到95%。

使用了两类不同的OF矩阵：

  • 单一值矩阵：所有条目初始化为相同的值，即对于所有的EF和R，OF(EF,R) := 1.5。
  • 预定值矩阵：OF条目根据不同的难度类别（Woiniak和Biedalak 1992）而变化：对于所有的EF，OF(EF, 1) := 5；对于所有的EF和R，OF(EF,R) := EF；其中EF的选择范围是1.3, 1.4, 1.5, . . . , 3.2（参见表一）。

预定矩阵OF旨在确保OF条目更快地收敛到其最优值，而单一值矩阵OF则用于验证优化算法的有效性。15%的项目根据单一值OF矩阵进行优化，85%的项目则使用预定OF矩阵进行安排。

使用了以下学习算法（请注意，重复可以无限期进行，并且OF矩阵的实验值可以随时获取，越晚越好）：

  1. 记忆一个新项目i：以自定进度的方式学习问题和答案之间的关联。
  2. 设置初始EF值：EFi := 2.5（设置对应于项目i的EF因子的初始值）。
  3. 设置重复次数：Ri := 1（将重复次数设置为1）。
  4. 确定首次重复日期：使用OF矩阵根据公式（1）确定首次重复的日期。
  5. 进行重复：在预定的重复日期，通过回答相关问题来重复该项目，并以0-5的等级评估回答的质量（表现良好则等级高）。
  6. 继续学习或停止：如果学习者希望继续学习，则Ri := Ri + 1；否则，停止。
  7. 调整EFi值：如果质量低于4，则降低EFi值；否则，增加。学习中出现问题的项目将被归类为更困难，因此会采用不同的重复间隔（详见Woiniak和Biedalak 1992）。
  8. 调整OF(EFi, Ri - 1)值：如果其应用导致质量低于4，则降低OF(EFi, Ri - 1)值；否则，增加。因此，不成功的重复会缩短学习中使用的间隔（调整变化速度以在重复中获得95%的稳定保留率；保留率下降将倾向于OF值较慢的向上变化和较快的向下变化，从而缩短重复中使用的间隔长度；详见Woiniak和Biedalak 1992）。
  9. 安排下一次重复或重置：如果质量大于或等于3，则根据公式（2）安排下一次重复并转到步骤5。如果质量低于3，则转到步骤3（该项目被视为遗忘）。

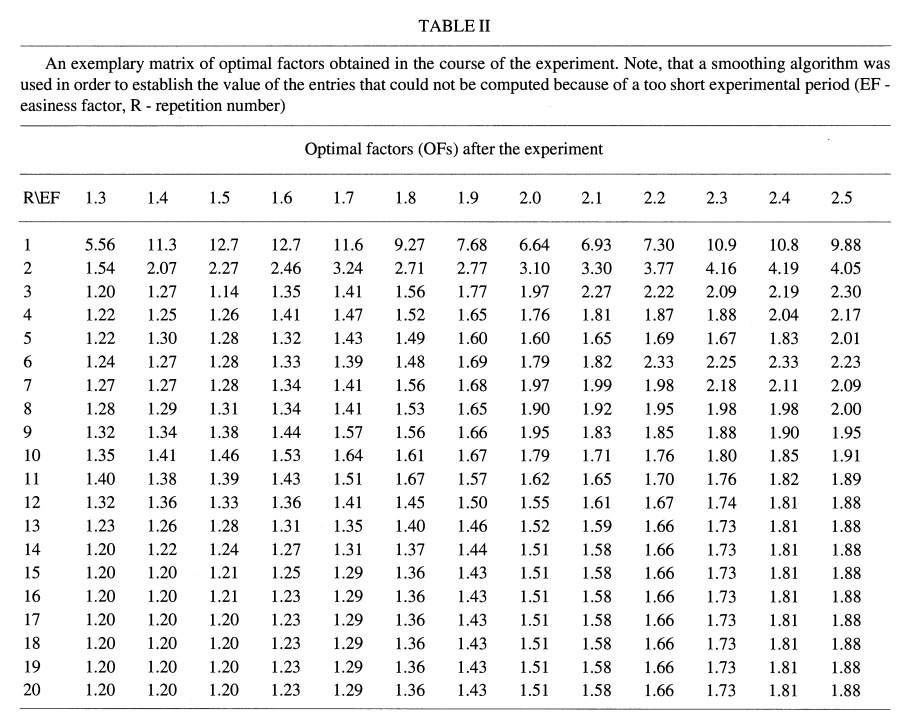
实验过程中产生的示例OF矩阵如表二所示（该矩阵来源于单一值OF矩阵）。

表二

数据处理

完成数据收集过程后，结果通过一系列逼近程序进行处理，这些程序旨在获得最适合的、可在课堂学习实践中使用的最优间隔累积函数.

针对95%知识保留率的最佳重复间隔函数，其通用公式已确定如下：

(3) 式:

$$ OI(EF, 1) = 5 $$ (4) 式: $$ OI(EF, R) = OI(EF, R - 1) * (EF - 0.1 + e^{-2.3*R + 5}) $$

公式中： $ EF $ - 表示一个待记忆项目的简单度因子。这个值通常在1.3（表示最难的项目）到2.8（表示最简单的项目）之间。 $ R $ - 代表重复的次数。 $ OI(EF, R) $ - 代表在第R次重复之前，针对难度系数为EF的项目的最佳间隔时长（单位：天）。

在公式 (3) 和 (4) 中，针对不同主题的函数参数之间的统计差异被认为不显著。同样，从单一值和预定值矩阵推导出的矩阵之间的差异也微不足道。这些结果明确表明，渐进式间隔优于集中式或分布式间隔。这在学习实践中具有应用价值，能够最大限度地减少记忆和保留所学材料所需的时间。

这项研究中使用的软件可免费从作者处获取，只需寄送一张3.5英寸、1.44 MB的软盘即可。

现在估计不行了 (

应用与实现

这是绘制的图像:
plot1

标签: none

添加新评论